10 分鐘就能搞懂！再質押是什麼？運作原理、必知風險一次看

前言

本文為 2023 年 11 月 13 日伊斯坦堡的 Restaking Summit 中的演講翻譯，Tarun Chitra 系統講解了再質押的定義，再質押與現有質押模式的本質對比，以及再質押在傳統金融中的位置類比，深入淺出地講解了再質押所承擔的風險本質和其它質押模式所承擔風險的具體區別。旨在幫助大家更好地瞭解再質押原理及背後所承擔的風險細節，只有在詳細瞭解風險本身之後，承擔風險才會「Less Scary」！

正文

本文一共約 4,000 字，一共有 5 個部分，閱讀完本文預計需要 10-15 分鐘。

1. 什麼是再質押（ReStaking）？
2. 再質押與……傳統金融?!
3. 我們如何減輕這些風險？
4. 再質押會帶來哪些風險？
5. 將再質押風險視覺化

一、什麼是再質押（ReStaking）？

當人們第一次聽到時會覺得再質押很有趣但令人困惑，這是因為不清楚額外風險來自何處。希望我們能在這裡嘗試解釋一些這些風險是什麼，以及不同的緩解方法是什麼，總體上讓風險變得不那麼可怕。我們今天聽了很多與再質押相關的討論，包括在相應場景中的應用。我想從最總體經濟的角度去看。接下來，我會簡要討論一些類似於傳統金融的事物，與此同時討論風險，我會確保不寫下數學等式，我們會看到一些圖表，然後談談如何去緩解這些風險。

這是 Vitalik 的定義，注意他使用了連字元，與其它用法不同。但實際上，這個想法是指某人有一種方法可以重復使用他們的權益，同時加入額外的罰沒（Slashing）規則，而這種權益與網路活動完全無關，只用於安全用途。

作為一個高層次的示意圖，你可以代入你是以太幣持有者，你通過 LST（Liquid Staking，流動性質押，以下簡稱 LST）或直接運行驗證器以參與網路，並在手續費和罰沒收入之間產生回饋循環。這是沒有再質押時的情況。

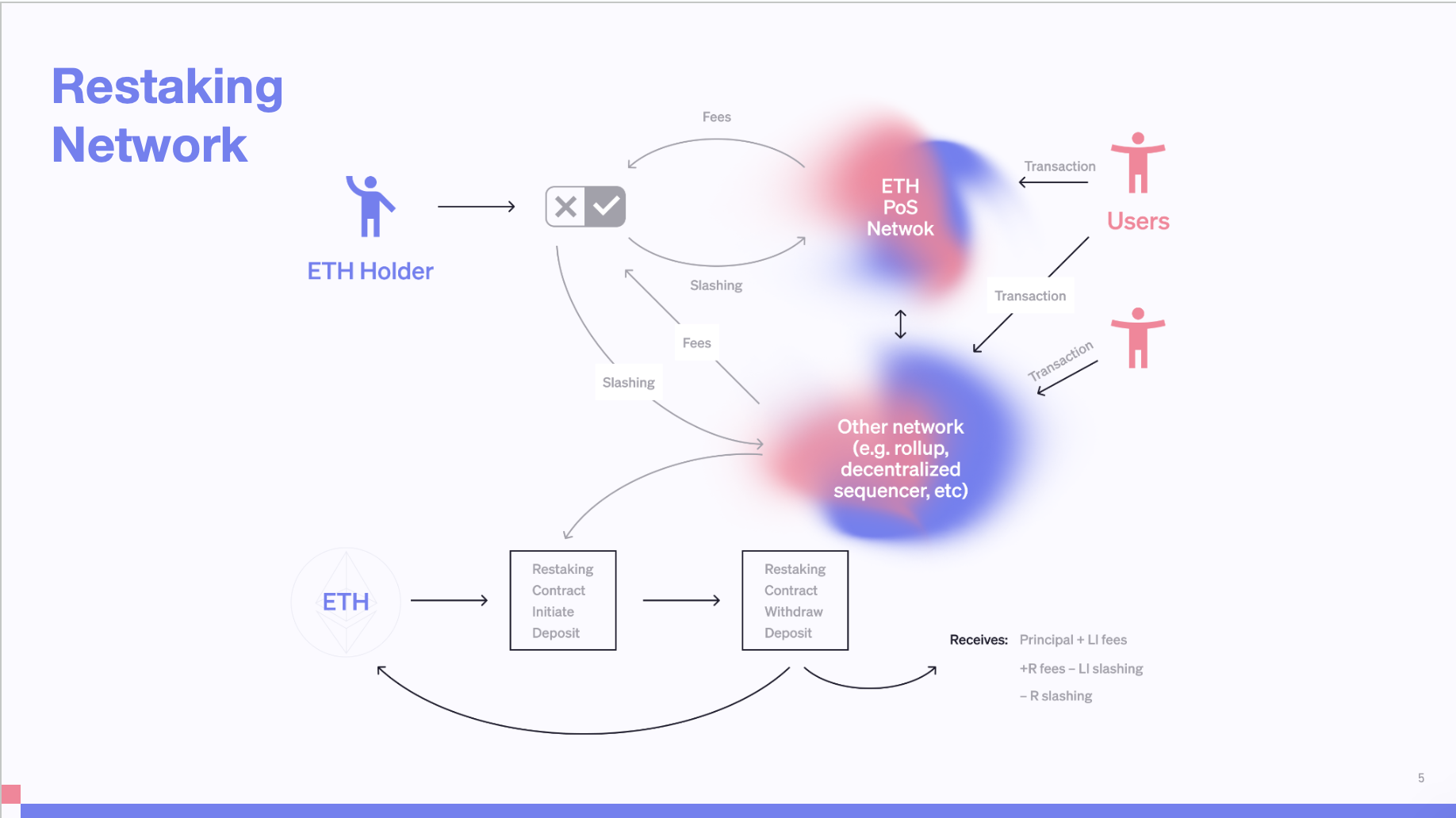
通過引入再質押，我們有了這些新的網路，如 MEV 拍賣和 FHE（Fully Homomorphic Encryption）。它們在處理手續費時引入了新的罰沒環節。這些環節由再質押委託合約觸發，該合約將資金存入質押合約。在再質押過程中，以太幣持有者的收益是本金加上 Layer1 手續費和再質押手續費，再減去任何 Layer1 和再質押的違規罰沒。

假設一個以太幣持有者擁有 100 枚以太幣並希望通過質押獲得 10% 的收益。他們將以太幣存入一個質押合約，如 Lido，並同意以太坊的罰沒規則，例如發送相互矛盾的消息（Equivocation）和雙簽。這樣，他們支持 Lido 驗證器並獲得 10% 的收益，但也可能面臨罰沒。

當持有者撤回時，他們獲得 107 枚以太幣。如果他們重新質押 100 枚以太幣，他們不僅從質押以太幣獲得 10% 的收益，還可以從再質押應用中獲得額外 5% 的收益。然而，與此同時，他們也面臨著新的風險。現在，罰沒事件呈現出一種樹狀的結構，有三種可能性。比如，人們可能在 Layer 1、Rollup、Layer 1 和 Rollup 上被罰沒。這表明使用者和驗證器正在選擇不同的風險路徑。與過去只有一組固定的 Layer1 罰沒事件相比，現在的狀態空間擴展了，使用者需要對風險有新的認識。

二、再質押與……傳統金融?!

這可能是聽起來不那麼有趣的一個概念：將再質押與傳統金融聯繫起來，但為什麼不呢？

再質押應用和 AVS（Actively Validated Service，主動驗證服務）在一定程度上類似於可驗證的公司債券。新興網路尋求 Layer1 的安全性，這有點像企業利用另一家公司的國家金融系統來發行債券以保護其資產。企業和主權國家基於最高的安全性和流動性發行債券。

例如，阿根廷仍然選擇發行以美元計價的債券，因為美元市場提供了最高的流動性和最廣泛的抵押購買機會。從這個角度來看，如果我們把以太幣看作是這類主權貨幣，那麼再質押應用程式就是向這一主權借貸，然後償還本金和利息。

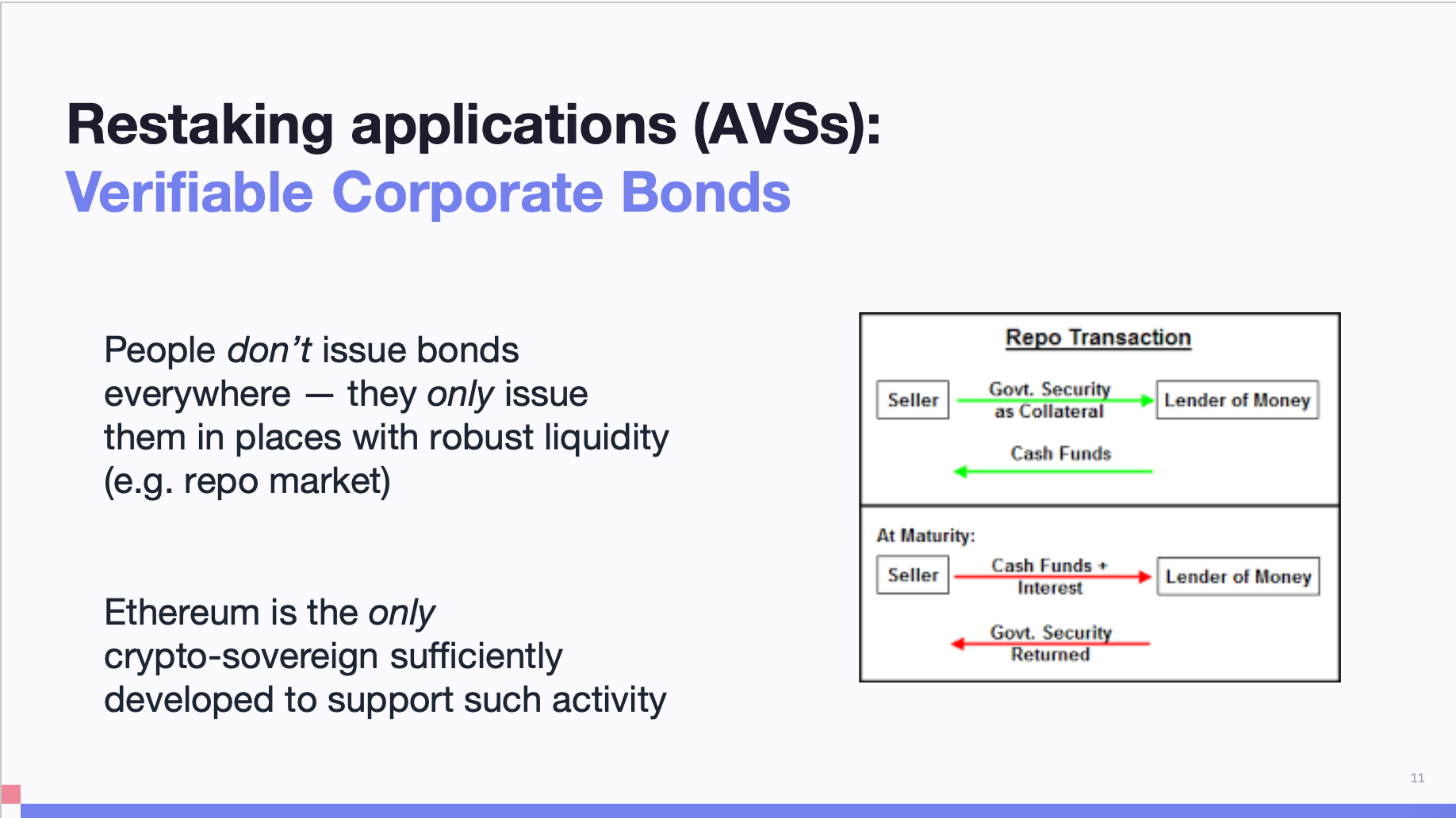
所以，人們不會在所有地方發行債券。如果看一下企業債券市場的歷史，你會發現它非常集中在少數幾個司法轄區。人們願意跨越自己的法律轄區去某個地方發行債券，因為那裡的流動性和退出機會好得多。

在回購市場中，人們可以用政府的國債或債券抵押借款：通過抵押債券，有人借給你錢；隨著時間的推移你逐步償還借款（如通過經營公司獲得的利潤）。例如空客或波音公司將大部分現金存放在主權債券中，然後在需要時將債券抵押借貸，以建社工廠或其它項目。

在 2023 年，以太坊是唯一一個能夠支持這種回購市場的主權實體。但我會認為再質押與傳統金融類型的區別之一是可驗證性，即違約事件，即當有人不支付時，實際上這是你觸發的違約罰沒規則之一，由密碼學激勵並且可以通過 Layer1 獨立驗證。

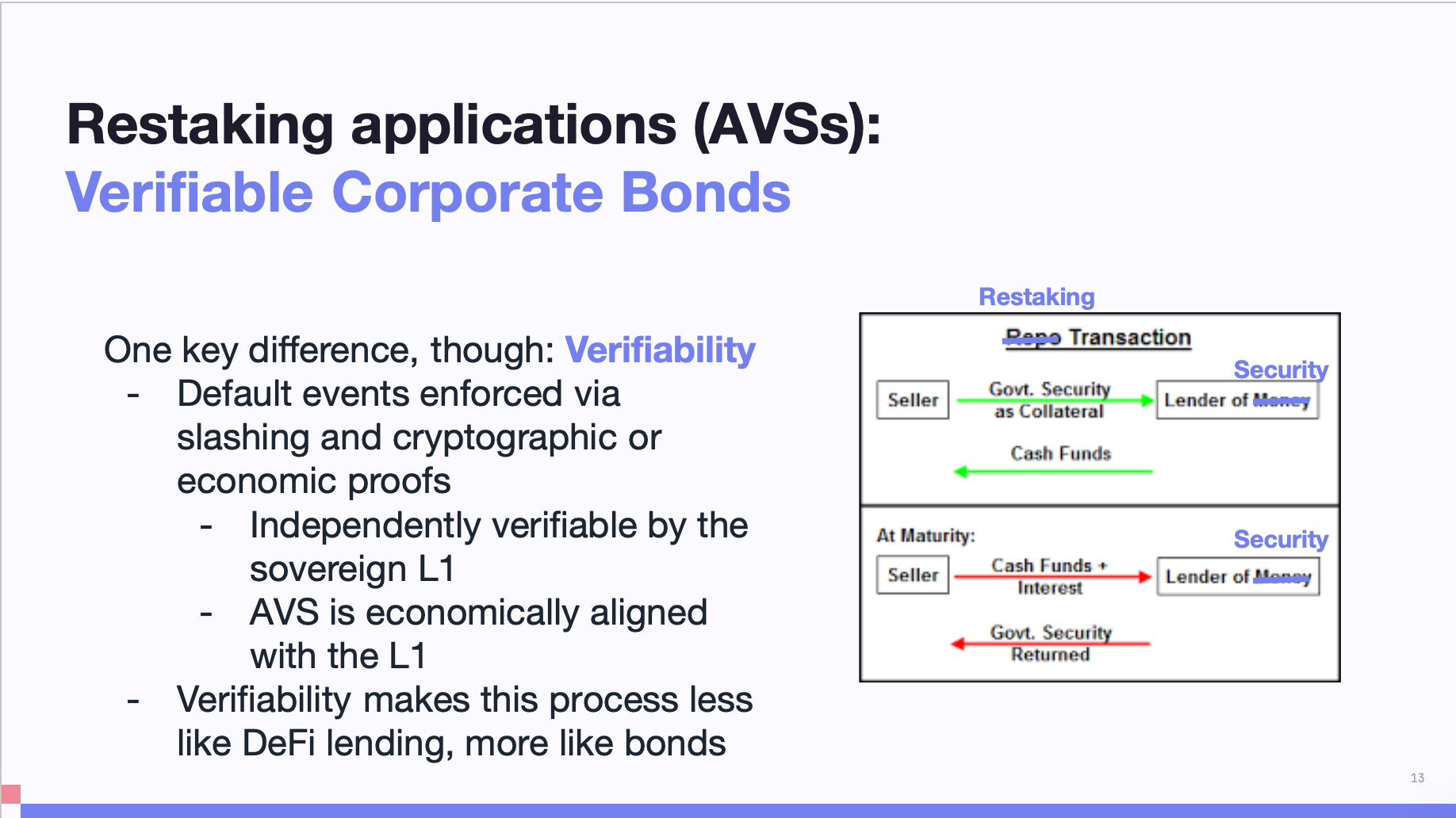
如果是政府交易（比如我購買了一堆國債，然後用它抵押借貸，但我後來沒有還貸款）那個人不太可能去找美國政府投訴。他可以通過嘗試提起訴訟，但他們沒有辦法證明我沒有支付，也不能說應該罰沒我的信用或立即進行懲罰。因此，債券發行者與借貸者在經濟激勵上並不一致。

而在 AVS 案例中，情況並非如此。在某種程度上，這使得這個過程更不像 DeFi 借貸，更像債券和債券市場。

三、再質押會帶來哪些風險？

好，下一個問題是，再質押帶來的風險本身是什麼？當然，我們在此略過智能合約和營運商風險。

在再質押的三種金融風險中，最嚴重的是罰沒風險，這是你直接失去本金的唯一方式。第二是流動性風險，很多再質押協議都有鎖定的 LST（流動性再質押代幣），現在如果 LST 的一大部分被鎖定在再質押池中，流動性的喪失意味著 LST 的價格相對於以太幣更加波動，AVS 的安全性是以 LST 來評估，因此對最終使用者來說，隱含波動性更高。當某 LST 的類型在 AVS 中過於集中時，就會出現這種流動性風險。

最後是集中化風險，以 DAO 駭客攻擊為例，假設三分之一的以太幣在單個 AVS 中，超過了傳統的 BFT 安全閾值。現在假設這個三分之一的以太幣可以通過並不是以太幣共識的規則來罰沒，比如說，我沒有提交詐欺證明，我被罰沒，而不是因為雙簽之類的事情。所以，從某種意義上說，集中化也意味著這兩個系統是耦合的。

四、將再質押風險視覺化

這些圖表展示的是隨時間變化的某個部位的價值，其中 Y 軸是部位的價值，X 軸是時間。紅線表示觸發違約的點，在所有這些情況下，違約都是最壞的情況，即本金完全歸零。我們將比較不同應用程式的一系列情況，並觀察它們的違約情況。

在鏈上借貸中，違約是一種指示函數跳躍至零的樣式，你有一個部位的價值，它低於某個清算閾值，然後跳躍至零。但這種跳躍是單一的，並且是一個隨機時間，所以它是一個根據實際過程而定的隨機停止時間，一次歸零。

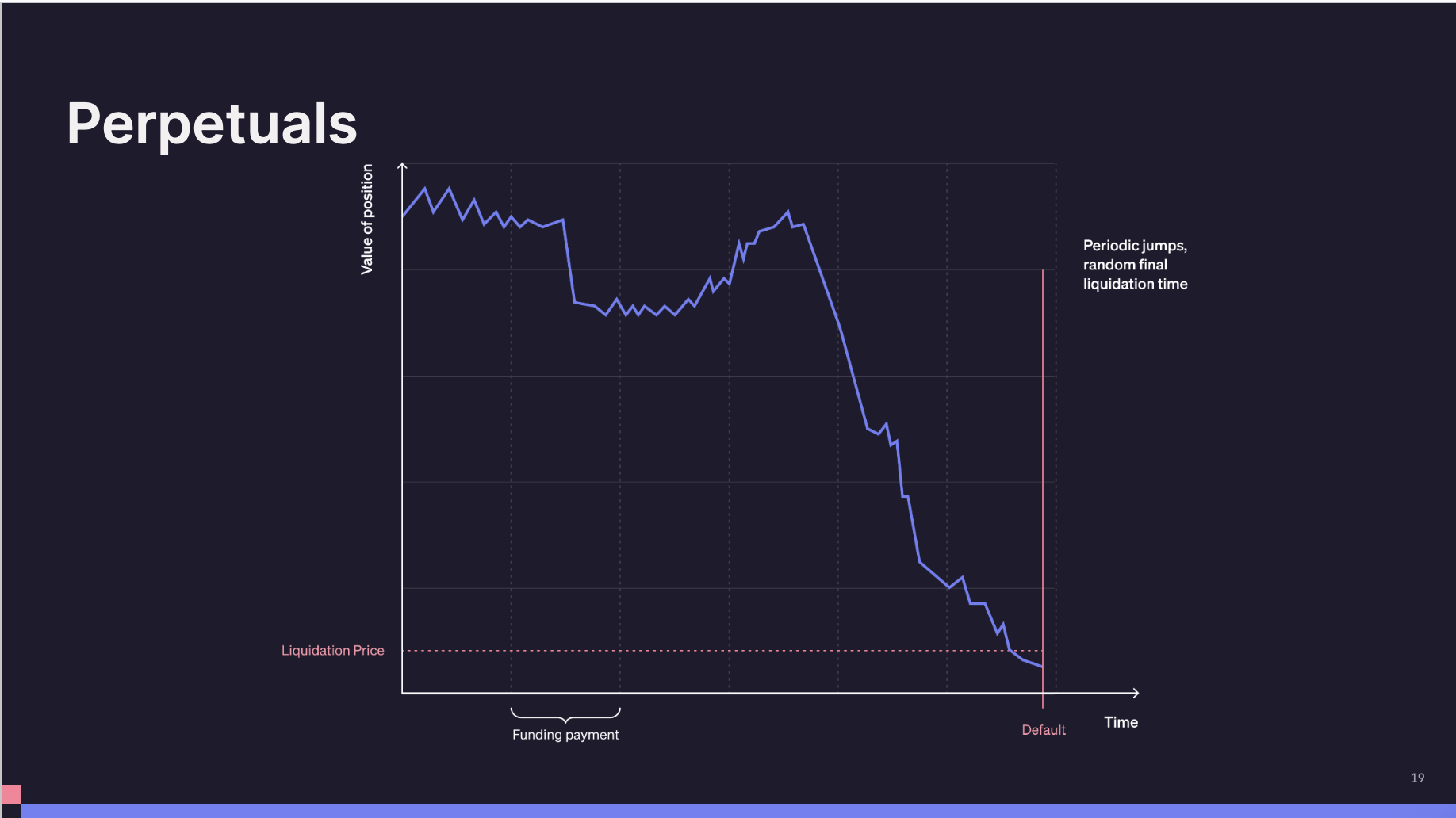
然後我們來考慮永續的情況，無論鏈上還是鏈下的永續組件，都有這種週期性的資金利率更新，但可能不容易看到這些資金支付時間。多頭和空頭之間的淨支付，或者空頭到多頭，會導致持倉價值的變化，所以你有這種週期性的跳躍，這些時間節點是幾乎接近違約（Default）的時間節點。

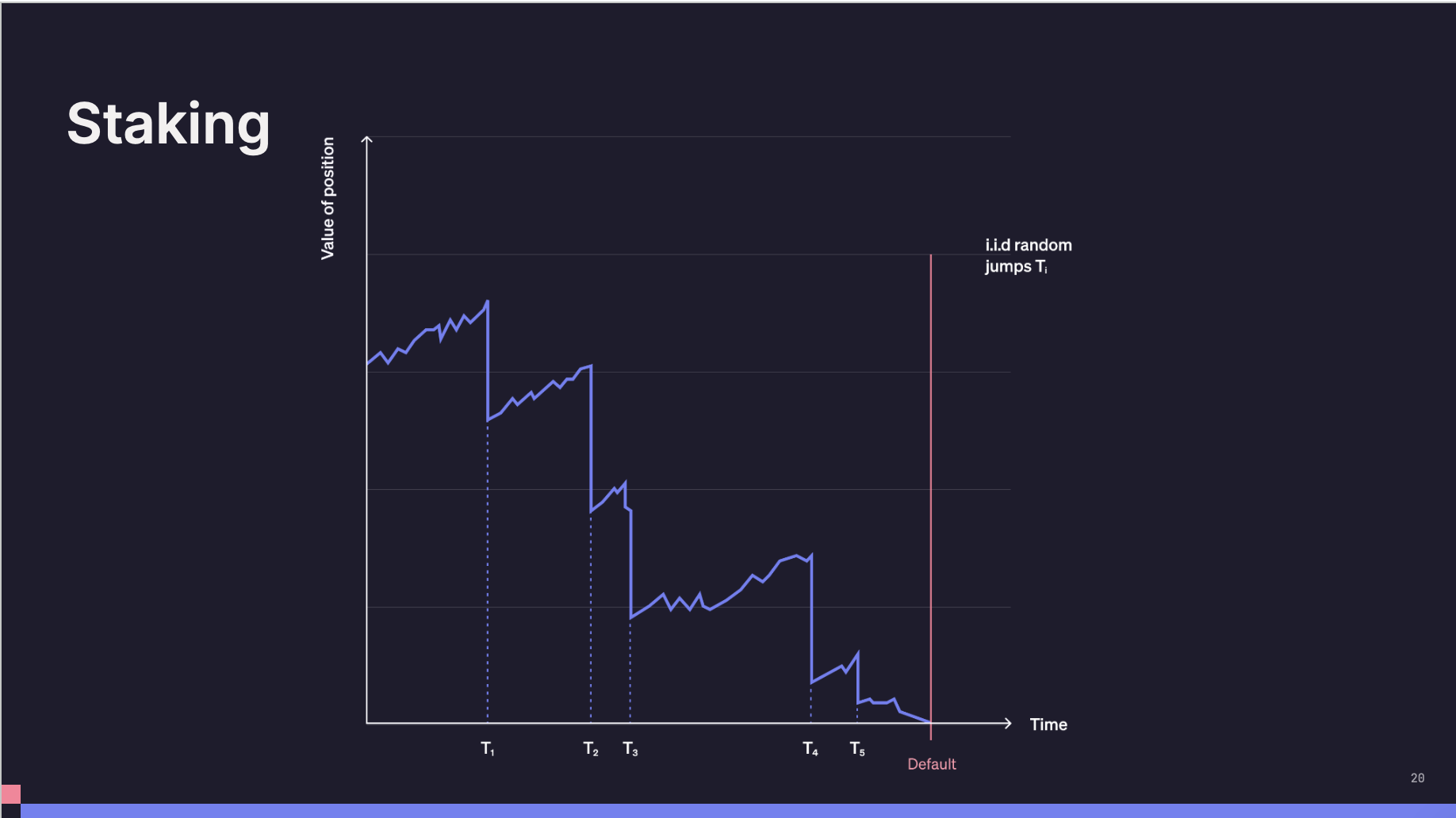
現在考慮普通的質押，所以在足夠去中心化的網路中足夠隔離的情況下，例如許多不同的節點，許多不同的覆蓋網路，不同的數據中心，不同的房屋，罰沒事件應該是 IID（Independent and identically distributed，獨立同分布）的，例如 AVS 某處的崩潰不會導致所有人同時被罰沒，當然實際上是不是 IID 就是一個經驗性問題了。但在這個模型的質押中，是足夠去中心化的，這些由於罰沒而導致的損失是 IID 事件。所以這個想法是，我鎖定的本金價值通常上漲，你可以看到，我有一個罰沒事件，它下跌，所以有這種情況，我的本金價值跳到零，但它們是獨立的，而且是隨機的。

最後一個問題是，再質押是什麼樣子？

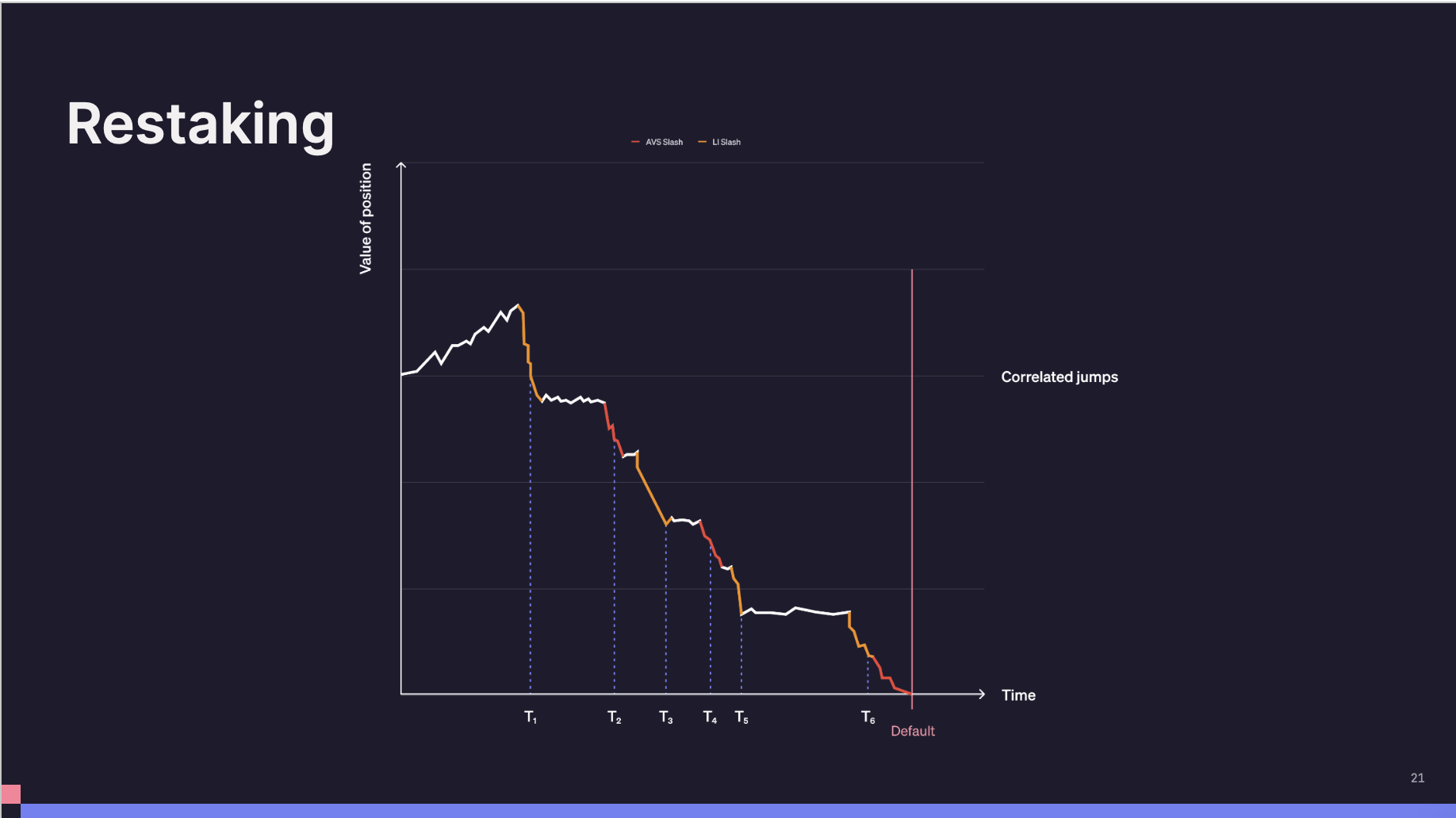
而再質押中你現在有這種相關的跳躍，這裡的想法是，當你考慮再質押時，你不能像考慮借貸或永續選擇權那樣，把它看作是在一個孤立的世界中。

因為在借貸中，你實際上只關心一個固定閾值和一個價格，比如說紫色線穿過紅色線的時間點；在永續選擇權中，你真正關心的是這些週期性間隔內價格的最大偏差。而在普通質押中，如果是 IID 的，你只在時間尺度相對於價值尺度很長時才相對安全，但在這裡不是這麼簡單。你需要認真考慮這兩個因素之間的相互作用。

所以有趣的是，在再質押中，你實際上可以複製之前所有的報酬率，再加上一些你不能複製的報酬率。

五、我們如何減輕這些風險？

所以，這就引出了自然的最後一個問題，那就是你到底應該怎麼做來緩解這些風險，你能做些什麼來確保這些相關事件不會太相關，並且這些跳躍不會太大。

實際上，你有兩個可以利用的工具。首先是參數優化，每個 AVS 都有一些參數，控制著 AVS 的安全性，無論是 TVL 上限，還是選擇罰沒規則。

如你在圖中注意到的，如果你注意到 AVS 的罰沒都是大致相同大小的，但你可以構造一些罰沒規則，這些規則在某些條件下可能會逐步成長或逐步減少，你在選擇罰沒的方式上有更多的自由，而在 Layer1 共識層方面你沒有那麼多（自由）。

再比如，如果你認同我提出的 AVS 實際上就是企業債券的類比，那麼流動性再質押代幣（LRT）就是一種債券基金，問題是如何對這種債券基金進行再平衡（Rebalancing），如何決定在 AVSs 之間重新分配資金。

實際上，上述的這兩件事情都是在修整這張圖片，讓它看起來（對投資人）更有利。

就是這樣，謝謝大家。

• 本文經授權轉載自：《PANews》
• 原文作者：Tarun Chitra, Guantlet